After going to all the trouble of explaining the “classical” analysis of the Tuesday’s Child problem, here I will explain why I think that analysis ends up with the wrong answer.
This will get into the nuts and bolts of the mathematics of probability again, but I will start with some of the questions which led me to rethink this problem.
In her Math Blog, Tanya Khovanova approaches the problem in a very interesting way. Paraphrasing Tanya, if Mr Smith tells you that one of his two children is a boy born on Tuesday, you will (if you accept the classical reasoning) revise the probability of two boys from 1/4 to 13/27. But, you would do the same if he said the boy was born on Wednesday, or indeed any day of the week. So if he said he had a boy born on *$$*@day (his voice was muffled and you couldn’t quite catch which day he said), wouldn’t you then revise your probability to 13/27 too? After all, you’d make that revision regardless of what day he actually said! If so, couldn’t you then revise the probability to 13/27 even if he doesn’t mention a day of the week and just said he had a boy? This clearly makes no sense and suggests there is a problem with the classical analysis.
The crux of the problem is that if Mr Smith is volunteering information, he could just as easily have spoken of a day other than Tuesday. Indeed, he may have said ‘I have two girls’, ‘Anyone for tennis?’ or ‘The UK doesn’t have a solvency problem the way Greece does’. The situation is very different if you are asking the questions of Mr Smith. If you ask him whether he has a boy born on Tuesday, he is restricted to saying ‘yes’ or ‘no’. At least, that’s the case if you allow the one big assumption I am making here, namely that whatever Mr Smith says, he is telling the truth (even about macroeconomics).
So, exactly how the information is revealed makes a difference. That in itself is well understood, but at this point many people will simply give up saying that there are too many options open to Mr Smith so it is impossible to come to any sensible conclusions. So, they will either give up on the problem or rephrase it to one that can be answered, such as where you ask the questions of Mr Smith, as I did in the Tuesday’s Child post. But, if you rephrase the problem, you are solving a different problem and giving up on the original one. What I will argue here is that all those options open to Mr Smith do not matter at all. Mathematically we can eliminate “irrelevant” options and come up with a perfectly defensible solution to the problem.
To ease into the mathematics, I will go back to Gardner’s simpler two boys problem:
Mr Smith says, ‘I have two children and at least one of them is a boy.’ What is the probability that the other child is a boy?
Before trying to answer that, I will instead ask if Mr Smith had two boys, what is the probability that he would say ‘I have two children and at least one of them is a boy’. It is impossible to say: there are so many other things he could have said instead. But what if I asked about the probability that Mr Smith would say ‘I have two children and at least one of them is a boy’. Again it’s impossible to say, so instead I will ask how does that probability compare to the probability of him saying ‘I have two children and at least one of them is a girl’? I would argue that, by symmetry, these two probabilities have to be the same (whatever they may be). As soon as you accept that, the classical solution falls apart.
Now for the mathematics. To save a bit of space I’ll use X to denote the event “Mr Smith says, ‘I have two children and at least one of them is a boy’.” and I will write Y for “Mr Smith says, ‘I have two children and at least one of them is a girl’.” In mathematical terms, my symmetry argument is that  , even though we don’t know what either of these probabilities are. This is the sort of reasoning I will use to calculate the conditional probability:
, even though we don’t know what either of these probabilities are. This is the sort of reasoning I will use to calculate the conditional probability:

Even though I will not be able to calculate either the top or the bottom term of this fraction, I will be able to calculate the ratio. To do this, I will use an equation I call “eliminating the irrelevant”. For any events A, B and Z, if A is a subset of Z and Z is independent of B then a bit of algebra will show that.
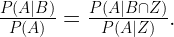
I can apply that to the current problem by setting 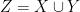 as long as Z is independent of BB. While we have not been told that is the case, it would seem to be an extremely reasonable assumption. If you think of all the other things Mr Smith might have said, is there any reason to assume that he would be more likely to say something other than X or Y simply because he had two boys rather than two girls? I don’t think so. It’s certainly possible that there could be a link, in much the same way that a coin could be biased, but in the absence of any other information we would start by assuming heads and tails are equally likely.
as long as Z is independent of BB. While we have not been told that is the case, it would seem to be an extremely reasonable assumption. If you think of all the other things Mr Smith might have said, is there any reason to assume that he would be more likely to say something other than X or Y simply because he had two boys rather than two girls? I don’t think so. It’s certainly possible that there could be a link, in much the same way that a coin could be biased, but in the absence of any other information we would start by assuming heads and tails are equally likely.
Note that Y by itself is not independent of BB, nor is X. What I am arguing is that the fact that Mr Smith has two boys (BB) does not affect the likelihood that he will say either X or Y as opposed to something else entirely.
The formula above thus allows us to calculate the conditional probability we are after as follows:

In one fell swoop, we have eliminated the irrelevant alternatives for Mr Smith and now have something we can work with, even though we will never know what the probability of X actually is!
The top line of the fraction is straightforward. If Mr Smith is restricted to X or Y and has two boys, only X is possible, so  . The bottom line requires a bit more work. As in the last post, we can break it up into disjoint alternatives:
. The bottom line requires a bit more work. As in the last post, we can break it up into disjoint alternatives:
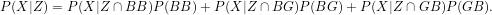
Note that I have taken the liberty of dropping one term here as I know that 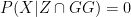 . By symmetry, since Mr Smith is restricted to X and Y,
. By symmetry, since Mr Smith is restricted to X and Y, 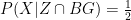 and the same applies for the GB term. So, we now have
and the same applies for the GB term. So, we now have
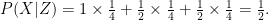
Now we’ve got everything we need and so
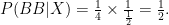
So instead of the classical conclusion that the probability that Mr Smith has two boys is 1/3, we have arrived at a figure of 1/2. The key to this result is that when we ask Mr Smith whether he has at least one boy, the probability that he says ‘yes’ is the same whether he has BB, BG or GB. When he makes an utterance of his own accord, although we don’t know what the probability values 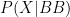 ,
, 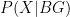 or
or 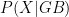 are, I am contending that
are, I am contending that 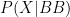 is double the other two (because in those cases he could have volunteered information about a girl). So, when Mr Smith volunteers that he has at least one boy, he is giving more information to us than if he simply answers ‘yes’ to our question.
is double the other two (because in those cases he could have volunteered information about a girl). So, when Mr Smith volunteers that he has at least one boy, he is giving more information to us than if he simply answers ‘yes’ to our question.
The same reasoning will also give a probability of 1/2 for two boys in the Tuesday’s child case (there you would set Z to cover the 14 options for Mr Smith of saying one of boy/girl and one of Monday/Tuesday/Wednesday, etc).
To sum up, if Mr Smith volunteers ‘I have two children and at least one is a boy,’ then the probability that he has two boys is 1/2, whereas if you ask him ‘do you have two children and at least one boy’ and he answers ‘yes’, the probability that he has two boys is 1/3. Likewise, if he volunteers that he has a boy born on a Tuesday, the probability that he has two boys is 1/2 but if you ask him whether he does and he says yes, the probability of two boys is 13/27.
This gives the satisfying (and, I think, intuitive) result that the day of the week does not matter and Tanya’s paradox of a muffled word changing the probabilities is resolved.





